Arithmetic And Geometric Sequences And Series
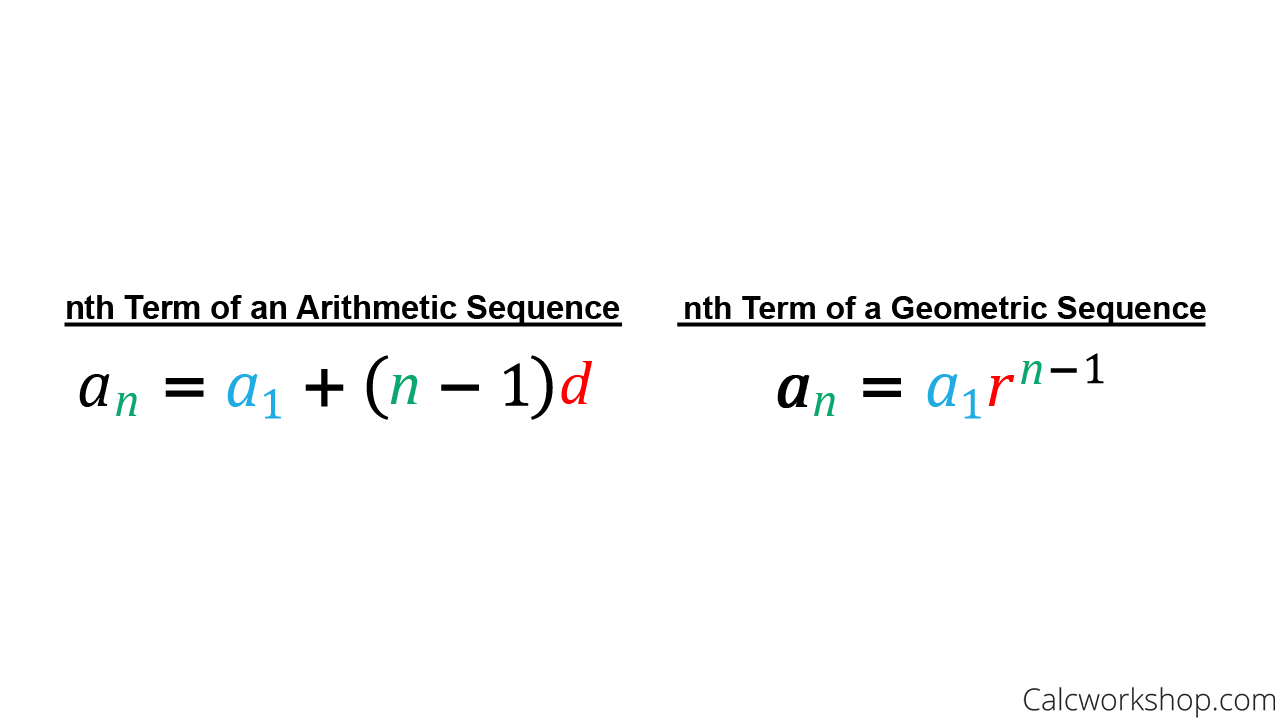
Arithmetic And Geometric Sequences 17 Amazing Examples Two common types of mathematical sequences are arithmetic sequences and geometric sequences. an arithmetic sequence has a constant difference between each consecutive pair of terms. this is similar to the linear functions that have the form y = mx b. y = m x b. a geometric sequence has a constant ratio between each pair of consecutive terms. Purplemath. the two simplest sequences to work with are arithmetic and geometric sequences. an arithmetic sequence goes from one term to the next by always adding (or subtracting) the same value. for instance, 2, 5, 8, 11, 14, is arithmetic, because each step adds three; and 7, 3, −1, −5, is arithmetic, because each step subtracts 4.

Arithmetic Geometric Sequence Along With Exmaples With Their Mean The sequences and series formulas for different types are tabulated below: arithmetic. sequence formula of the n th term. a n = a (n 1) d. series formula for the sum of n terms. s n = n 2 (2a (n 1) d) geometric. sequence formula of the n th term. Exercise 9.3.3. find the sum of the infinite geometric series: ∑∞ n = 1 − 2(5 9)n − 1. answer. a repeating decimal can be written as an infinite geometric series whose common ratio is a power of 1 10. therefore, the formula for a convergent geometric series can be used to convert a repeating decimal into a fraction. We will now do the same for geometric sequences. the sum, sn, of the first n terms of a geometric sequence is written as sn = a1 a2 a3 … an. we can write this sum by starting with the first term, a1, and keep multiplying by r to get the next term as: sn = a1 a1r a1r2 … a1rn − 1. We found the sum of both general sequences and arithmetic sequence. we will now do the same for geometric sequences. the sum, sn, of the first n terms of a geometric sequence is written as sn = a1 a2 a3 an. we can write this sum by starting with the first term, a1, and keep multiplying by r to get the next term as:.

Arithmetic Sequence Vs Geometric Sequence Youtube We will now do the same for geometric sequences. the sum, sn, of the first n terms of a geometric sequence is written as sn = a1 a2 a3 … an. we can write this sum by starting with the first term, a1, and keep multiplying by r to get the next term as: sn = a1 a1r a1r2 … a1rn − 1. We found the sum of both general sequences and arithmetic sequence. we will now do the same for geometric sequences. the sum, sn, of the first n terms of a geometric sequence is written as sn = a1 a2 a3 an. we can write this sum by starting with the first term, a1, and keep multiplying by r to get the next term as:. An arithmetic geometric progression (agp) is a progression in which each term can be represented as the product of the terms of an arithmetic progressions (ap) and a geometric progressions (gp). in the following series, the numerators are in ap and the denominators are in gp:. The recursive definition for the geometric sequence with initial term a and common ratio r is an = an ⋅ r; a0 = a. to get the next term we multiply the previous term by r. we can find the closed formula like we did for the arithmetic progression. write. a0 = a a1 = a0 ⋅ r a2 = a1 ⋅ r = a0 ⋅ r ⋅ r = a0 ⋅ r2 ⋮.
Arithmetic Sequences And Geometric Sequences An arithmetic geometric progression (agp) is a progression in which each term can be represented as the product of the terms of an arithmetic progressions (ap) and a geometric progressions (gp). in the following series, the numerators are in ap and the denominators are in gp:. The recursive definition for the geometric sequence with initial term a and common ratio r is an = an ⋅ r; a0 = a. to get the next term we multiply the previous term by r. we can find the closed formula like we did for the arithmetic progression. write. a0 = a a1 = a0 ⋅ r a2 = a1 ⋅ r = a0 ⋅ r ⋅ r = a0 ⋅ r2 ⋮.

Comments are closed.